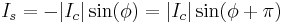Pi Josephson junction

A Josephson Junction is a voltage-to-frequency converter usefully sensitive to voltage, current and magnetic fields that is made of a superconducting wire interrupted by an insulating weak-link. A 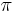$\pi$ Josephson junction is a specific example of a Josephson junction which has a Josephson phase φ of 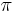$\pi$ in the ground state when no external current or magnetic field is applied.

1 Background
2 Technologies and physical principles
3 Historical developments
4 See also
5 References

Background

The supercurrent I_s through a conventional Josephson junction (JJ) is given by I_s = I_csin(φ), where φ is the phase difference of the superconducting wave functions of the two electrodes, i.e. the Josephson phase.^[1] The critical current I_c is the maximum supercurrent that can flow through the Josephson junction. In experiment, one usually applies some current through the Josephson junction and the junction reacts by changing the Josephson phase. From the above formula it is clear that the phase φ = arcsin(I/I_c), where I is the applied (super)current.

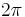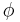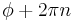Since the phase is $2\pi$ -periodic, i.e. $\phi$ and $\phi%2B2\pi n$ are physically equivalent, without losing generality, we restrict the discussion below to the interval 0 < φ < 2 $\pi$ .

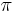When no current (I = 0) is passing through the Josephson junction, e.g. when the junction is disconnected, the junction is in the ground state and the Josephson phase across it is zero (φ = 0). The phase can also be 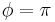$\phi=\pi$ , also resulting in no current through the junction. It turns out that the state with 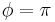$\phi=\pi$ is unstable and corresponds to the Josephson energy maximum, while the state φ = 0 corresponds to the Josephson energy minimum and is a ground state.

In certain cases one may obtain a Josephson junction where the critical current is negative (I_c < 0). In this case, the first Josephson relation becomes

$I_s = -|I_c|\sin(\phi) = |I_c|\sin(\phi%2B\pi)$

Obviously, the ground state of such a Josephson junction is 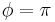$\phi=\pi$ and corresponds to the Josephson energy minimum, while the conventional state φ = 0 is unstable and corresponds to the Josephson energy maximum. Such a Josephson junction with 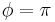$\phi=\pi$ in the ground state is called a $\pi$ Josephson junction.

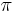$\pi$ Josephson junctions have quite unusual properties. For example, if one connects (shorts) the superconducting electrodes with the inductance L (e.g. superconducting wire), one may expect the spontaneous supercurrent circulating in the loop, passing through the junction and through inductance clockwise or counterclockwise. This supercurrent is spontaneous and belongs to the ground state of the system. The direction of its circulation is chosen at random. This supercurrent will of course induce a magnetic field which can be detected experimentally. The magnetic flux passing through the loop will have the value from 0 to a half of magnetic flux quanta, i.e. from 0 to Φ₀/2, depending on the value of inductance L.

Technologies and physical principles

Ferromagnetic Josephson junctions. Consider a Josephson junction with a ferromagnetic Josephson barrier, i.e. the multilayers Superconductor-Ferromagnet-Superconductor (SFS) or Superconductor-Insulator-Ferromagnet-Superconductor (SIFS). In such structures the superconducting order parameter inside the F-layer oscillates in the direction perpendicular to the junction plane. As a result, for certain thicknesses of the F-layer and temperatures, the order parameter may become +1 at one superconducting electrode and -1 at the other superconducting electrode. In this situation one gets a 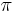$\pi$ Josephson junction. Note that inside the F-layer the competition of different solutions takes place and the one with the lower energy wins out. Various ferromagnetic 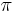$\pi$ junctions have been fabricated: SFS junctions with weak ferromagnetic interlayers;^[2] SFS junctions with strong ferromagnetic interlayers, such as Co, Ni^[3], and NiFe^[4] SIFS junctions;^[5] ^[6] and S-Fi-S junctions.^[7]

Josephson junctions with unconventional order parameter symmetry. Novel superconductors, notably high temperature cuprate superconductors, have an anisotropic superconducting order parameter which can change its sign depending on the direction. In particular, a so-called d-wave order parameter has a value of +1 if one looks along the crystal axis a and –1 if one looks along the crystal axis b. If one looks along the ab direction (45° between a and b) the order parameter vanishes. By making Josephson junctions between d-wave superconducting films with different orientations or between d-wave and conventional isotropic s-wave superconductors, one can get a phase shift of 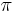. Nowadays there are several realizations of 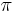Josephson junctions of this type:
- tri-crystal grain boundary Josephson junctions,^[8]
- tetra-crystal grain boundary Josephson junctions,^[9]
- d-wave/s-wave ramp zigzag JJs Josephson junctions,^[10]^[11]^[12]^[13]
- tilt-twist grain boundary Josephson junctions,^[14]
- p-wave based Josephson junctions.

Superconductor-NormalMetal-Superconductor (SNS) Josephson junctions with nonequlibrium electron distribution in N-layer.^[15]

Superconductor-Quantum Dot-Superconductor (S-QuDot-S) Josephson junctions (implemented by carbon nanotube Josephson junctions).^[16]

Historical developments

Theoretically, the first time the possibility of creating a 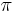$\pi$ Josephson junction was discussed by Bulaevskii et al. ,^[17] who considered a Josephson junction with paramagnetic scattering in the barrier. Almost one decade later, the possibility of having a 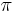$\pi$ Josephson junction was discussed in the context of heavy fermion p-wave superconductors.^[18]

Experimentally, the first 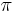$\pi$ Josephson junction was a corner junction made of yttrium barium copper oxide (d-wave) and Pb (s-wave) superconductors.^[10] The first unambiguous proof of a 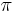$\pi$ Josephson junction with a ferromagnetic barrier was given only a decade later.^[2] That work used a weak ferromagnet consisting of an copper-nickel alloy (Cu_xNi_1-x, with x around 0.5) and optimized it so that the Curie temperature was close to the superconducting transition temperature of the superconducting niobium leads.

References

^ B. D. Josephson (1962). "Possible New Effects in Superconducting Tunnelling". Phys. Lett. 1 (7): 251. Bibcode 1962PhL.....1..251J. doi:10.1016/0031-9163(62)91369-0.
^ ^a ^b V.V.Ryazanov, V.A.Oboznov, A.Yu.Rusanov, A.V.Veretennikov, A.A.Golubov and J.Aarts (2001). "Coupling of two superconductors through a ferromagnet: evidence of a 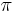$\pi$ -junction". Phys. Rev. Lett 86 (11): 2427–30. arXiv:cond-mat/0008364. Bibcode 2001PhRvL..86.2427R. doi:10.1103/PhysRevLett.86.2427. PMID 11289946.
^ A. A. Bannykh, J. Pfeiffer, V. S. Stolyarov, I. E. Batov, V. V. Ryazanov, and M. Weides (2009). "Josephson tunnel junctions with a strong ferromagnetic interlayer". Phys. Rev. B 79 (5): 054501. Bibcode 2009PhRvB..79e4501B. doi:10.1103/PhysRevB.79.054501.
^ J.W.A. Robinson, S. Piano, G. Burnell, C. Bell and M. G. Blamire (2006). "Critical Current Oscillations in Strong Ferromagnetic 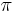$\pi$ Junctions". Phys. Rev. Lett 97 (17): 177003. arXiv:cond-mat/0606067. Bibcode 2006PhRvL..97q7003R. doi:10.1103/PhysRevLett.97.177003. PMID 17155498.
^ T. Kontos, M. Aprili, J. Lesueur and X. Grison (2002). "Josephson Junction through a Thin Ferromagnetic Layer: Negative Coupling". Phys. Rev. Lett. 89 (13): 137007. Bibcode 2002PhRvL..89m7007K. doi:10.1103/PhysRevLett.89.137007. PMID 12225057.
^ M. Weides, M. Kemmler, H. Kohlstedt, A. Buzdin, E. Goldobin, D. Koelle, and R. Kleiner (2006). "High quality ferromagnetic 0 and pi Josephson tunnel junctions". Appl. Phys. Lett. 89 (12): 122511. arXiv:cond-mat/0604097. Bibcode 2006ApPhL..89l2511W. doi:10.1063/1.2356104.
^ O. Vavra, S. Gazi, D. S. Golubovic, I. Vavra, J. Derer, J. Verbeeck, G. Van Tendeloo, V. V. Moshchalkov (2006). "0 and 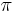$\pi$ phase Josephson coupling through an insulating barrier with magnetic impurities". Phys. Rev. B 74 (2): 020502,. arXiv:cond-mat/0606513. Bibcode 2006PhRvB..74b0502V. doi:10.1103/PhysRevB.74.020502.
^ Tsuei, C. C.; Kirtley, J. R. (2000). "Pairing symmetry in cuprate superconductors". Rev. Mod. Phys. 72 (4): 969–1016. Bibcode 2000RvMP...72..969T. doi:10.1103/RevModPhys.72.969.
^ B. Chesca (1999). Annalen Physik (Leipzig) 8: 511.
^ ^a ^b Van Harlingen, D. J. (1995). "Phase-sensitive tests of the symmetry of the pairing state in the high-temperature superconductors—Evidence for dx^2-y^2 symmetry". Reviews of Modern Physics 67 (2): 515. Bibcode 1995RvMP...67..515V. doi:10.1103/RevModPhys.67.515.
^ Smilde, H. J. H. (2002). "d-Wave–Induced Josephson Current Counterflow in YBa_{2}Cu_{3}O_{7}/Nb Zigzag Junctions". Physical Review Letters 88: 057004. Bibcode 2002PhRvL..88e7004S. doi:10.1103/PhysRevLett.88.057004.
^ Hilgenkamp, Hans; Ariando; Smilde, Henk-Jan H.; Blank, Dave H. A.; Rijnders, Guus; Rogalla, Horst; Kirtley, John R.; Tsuei, Chang C. (2003). "Ordering and manipulation of the magnetic moments in large-scale superconducting π-loop arrays". Nature 422 (6927): 50–3. Bibcode 2003Natur.422...50H. doi:10.1038/nature01442. PMID 12621428.
^ Ariando (2005). "Phase-Sensitive Order Parameter Symmetry Test Experiments Utilizing Nd_{2-x}Ce_{x}CuO_{4-y}/Nb Zigzag Junctions". Physical Review Letters 94: 167001. arXiv:cond-mat/0503429. Bibcode 2005PhRvL..94p7001A. doi:10.1103/PhysRevLett.94.167001.
^ Lombardi, F. (2002). "Intrinsic d-Wave Effects in YBa_{2}Cu_{3}O_{7-δ} Grain Boundary Josephson Junctions". Physical Review Letters 89: 207001. Bibcode 2002PhRvL..89t7001L. doi:10.1103/PhysRevLett.89.207001.
^ J. J. A. Baselmans, A. F. Morpurgo, B. J. Van Wees, T. M. Klapwijk (1999). "Reversing the direction of the supercurrent in a controllable Josephson junction". Nature 397 (6714): 43–45. Bibcode 1999Natur.397...43B. doi:10.1038/16204.
^ J-P. Cleuziou, W. Wernsdorfer, V. Bouchiat, T. Ondarçuhu, M. Monthioux (2006). "Carbon nanotube Superconducting Quantum Interference Device". Nature Nanotechnology 1 (1): 53–9. Bibcode 2006NatNa...1...53C. doi:10.1038/nnano.2006.54. PMID 18654142.
^ L. N. Bulaevskii, V. V. Kuzii, A. A. Sobyanin; Kuziǐ; Sobyanin (1977). "Superconducting system with weak coupling to the current in the ground state". JETP Lett. 25: 290–294,. Bibcode 1977JETPL..25..290B.
^ V. B. Geshkenbein, A. I. Larkin, A. Barone (1987). "Vortices with half magnetic flux quanta in heavy-fermion superconductors". Phys. Rev. B 36: 235–238. Bibcode 1987PhRvB..36..235G. doi:10.1103/PhysRevB.36.235.

Pi Josephson junction

Contents

Background

Technologies and physical principles

Historical developments

See also

References